7.1分式(2)
图片预览



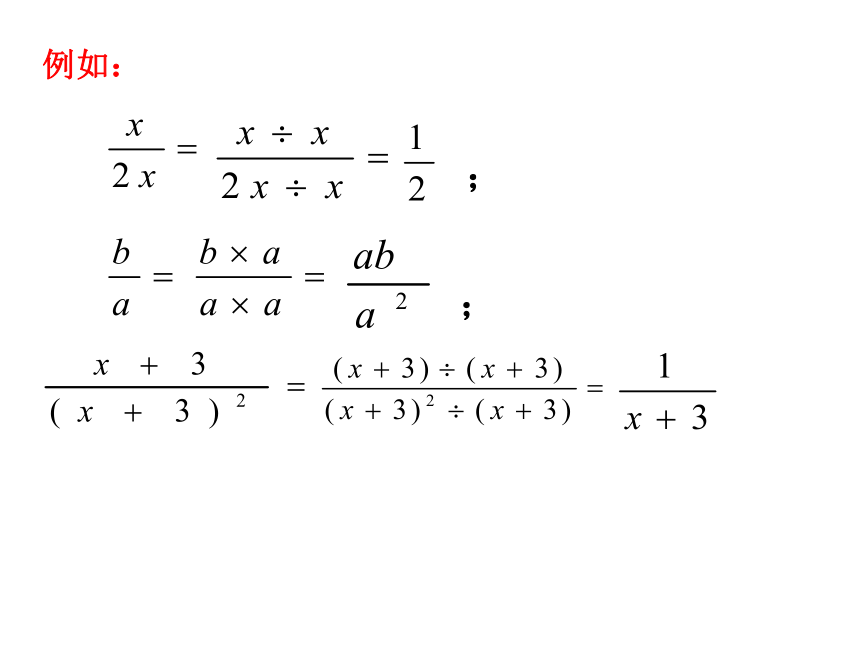



文档简介
(共20张PPT)
7.1(2)分式的基本性质
= =
分数的分子与分母都乘以或除以同一个不等于零的数,分数的值不变.
那么分式有没有类似的性质呢?
这是根据什么呢?
分数的基本性质:
= =
当 =3时,分式 的值为多少?
用实验来说明
2、实验过程
1 、分式 是否具有与分数类似的基本性质
说明: = 换几个数再试一试
把除改成乘呢
当 x =3时,分式 的值为多少?
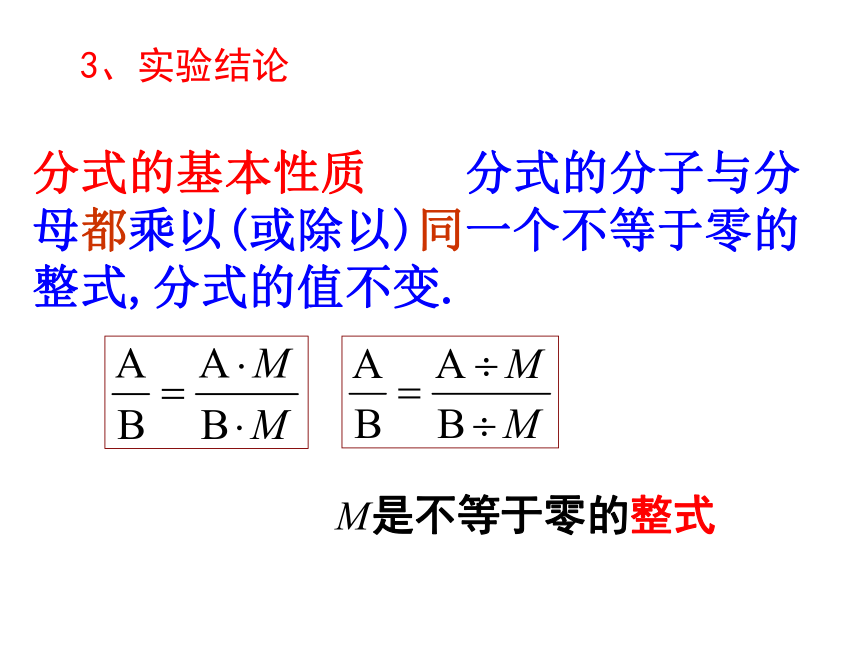
是不等于零的整式
分式的基本性质 分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
3、实验结论
例如:
;
;
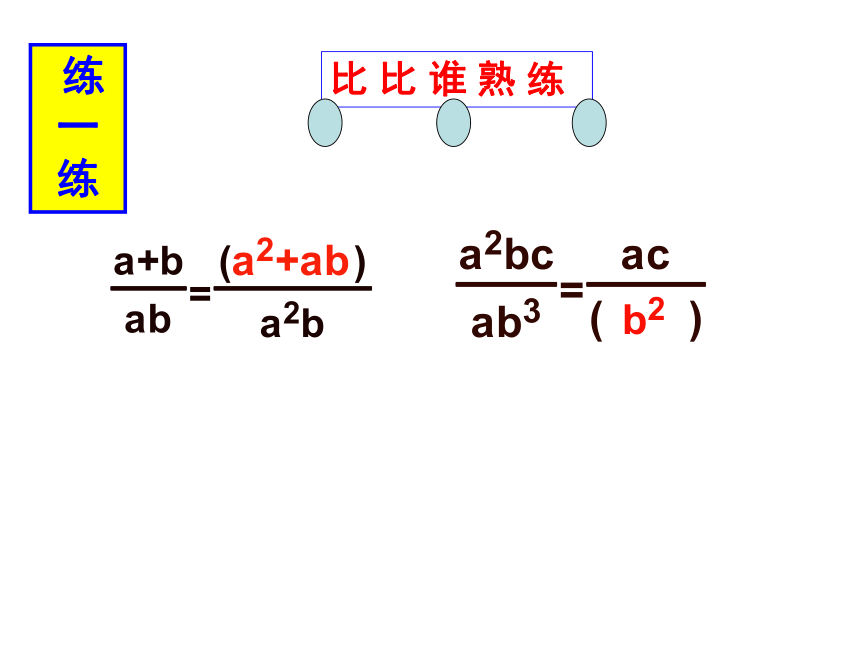
练 一练
比 比 谁 熟 练
下列各式从左边变形到右边是否正确,
并说明理由:
分式的分子与分母都 乘以(或除以)同一个不等于零的整式,分式的值不变
分式性质的应用(1)处理符号
探究分式的符号变化与分式的值之间的关系
①
观察分式:
,
,
你认为这三个分式的值相等吗 发现了分式的符号有几个地方可以放置?
② 请在下列各式中找出哪些是相等的式子?
你认为在分式中分子,分母的符号可以移到什么地方
不改变分式的值,使下列各式的分子与分母都不含有“-”号。
2、不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数:
当分子或者分母是多项式时:
(2)若最高次项的系数为负数,则提出“-”号并加括号,注意括号内的各项都要变号。
(1)按同一字母的降幂排列,
可要区分项的符号与分子分母的符号哦!
1、不改变分式的值,把下列各式的分子、分母中各项的系数都化为整数。
当系数是小数时:一般情况下,分式的分子、分母都乘以10的倍数。
当系数是分数时:分式的分子、分母都乘以每一项系数的分母的最小公倍数;
分式基本性质应用(2)
练习:157页做一做1
例1:化简分式
基本步骤:
(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
把分式分子、分母的 公因式约去,这种变 形叫分式的约分.
分式基本性质应用(3)约分
在化简(1)时同学甲和同学乙出现了分歧
同学甲
同学乙
分式约分之后分子与分母不再有公因式,此时的分式就叫做最简分式。
注意:约分一定要把公因式约完,约分的结果应是最简分式或整式。
小 医生
诊断下列分式的变形是否有“病”
-
x+y
y
≠
=
-x+1
x+1
完成书本158页课内练习3
1、如果把分式
中的字母x,y扩大为原来的2倍,则分
式的值( )
练一练:
A、缩小为原来的 B、扩大到原来2倍
C、不变 D、缩小为原来的
2、如果把上题分式 改为
那么答案又是什么呢?( )
c
A
有一道题目:当X=4时,求分式 的值。小红是这样解的:
你认为小红的解答对吗?如果不正确,请说明理由,并给出正确的解答。
小 结
1、这堂课你收获了哪些数学知识?
7.1(2)分式的基本性质
= =
分数的分子与分母都乘以或除以同一个不等于零的数,分数的值不变.
那么分式有没有类似的性质呢?
这是根据什么呢?
分数的基本性质:
= =
当 =3时,分式 的值为多少?
用实验来说明
2、实验过程
1 、分式 是否具有与分数类似的基本性质
说明: = 换几个数再试一试
把除改成乘呢
当 x =3时,分式 的值为多少?
是不等于零的整式
分式的基本性质 分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
3、实验结论
例如:
;
;
练 一练
比 比 谁 熟 练
下列各式从左边变形到右边是否正确,
并说明理由:
分式的分子与分母都 乘以(或除以)同一个不等于零的整式,分式的值不变
分式性质的应用(1)处理符号
探究分式的符号变化与分式的值之间的关系
①
观察分式:
,
,
你认为这三个分式的值相等吗 发现了分式的符号有几个地方可以放置?
② 请在下列各式中找出哪些是相等的式子?
你认为在分式中分子,分母的符号可以移到什么地方
不改变分式的值,使下列各式的分子与分母都不含有“-”号。
2、不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数:
当分子或者分母是多项式时:
(2)若最高次项的系数为负数,则提出“-”号并加括号,注意括号内的各项都要变号。
(1)按同一字母的降幂排列,
可要区分项的符号与分子分母的符号哦!
1、不改变分式的值,把下列各式的分子、分母中各项的系数都化为整数。
当系数是小数时:一般情况下,分式的分子、分母都乘以10的倍数。
当系数是分数时:分式的分子、分母都乘以每一项系数的分母的最小公倍数;
分式基本性质应用(2)
练习:157页做一做1
例1:化简分式
基本步骤:
(1)若分子﹑分母都是单项式,则约简系数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
把分式分子、分母的 公因式约去,这种变 形叫分式的约分.
分式基本性质应用(3)约分
在化简(1)时同学甲和同学乙出现了分歧
同学甲
同学乙
分式约分之后分子与分母不再有公因式,此时的分式就叫做最简分式。
注意:约分一定要把公因式约完,约分的结果应是最简分式或整式。
小 医生
诊断下列分式的变形是否有“病”
-
x+y
y
≠
=
-x+1
x+1
完成书本158页课内练习3
1、如果把分式
中的字母x,y扩大为原来的2倍,则分
式的值( )
练一练:
A、缩小为原来的 B、扩大到原来2倍
C、不变 D、缩小为原来的
2、如果把上题分式 改为
那么答案又是什么呢?( )
c
A
有一道题目:当X=4时,求分式 的值。小红是这样解的:
你认为小红的解答对吗?如果不正确,请说明理由,并给出正确的解答。
小 结
1、这堂课你收获了哪些数学知识?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
