浙教版七年级下册1.3 平行线的判定(1)课件(18张ppt)
文档属性
| 名称 | 浙教版七年级下册1.3 平行线的判定(1)课件(18张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 802.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-30 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
1.3平行线的判定(1)
教学目标
从“用三角尺和直尺画平行线”的活动过程中发现基本事实:同位角相等,两直线平行。
掌握基本事实:同位角相等,两直线平行。
会运用基本事实及其推论判断两直线平行,会进行简单的推理和表述。
教学重点
掌握“同位角相等,两直线平行”的判定方法
教学难点
例1中,需先将已知条件作适当的转化,说理过程要求有条理的表述。这方面能力,学生较薄弱。
温故知新
(1)平面内两条直线的位置关系有几种?
(2)过已知直线外一点画已知直线的平行线
完成P11作业题4
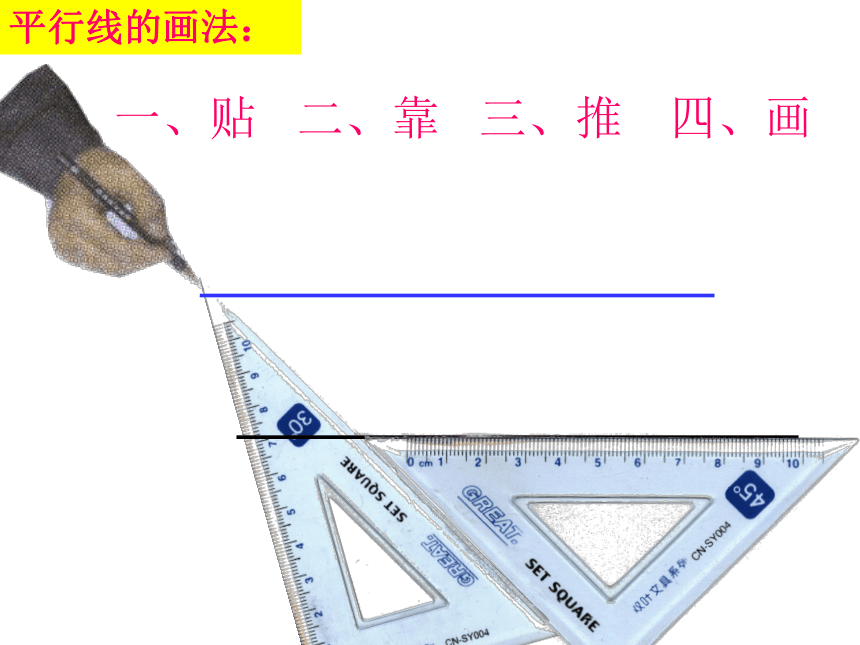
一、贴
二、靠
三、推
四、画
平行线的画法:
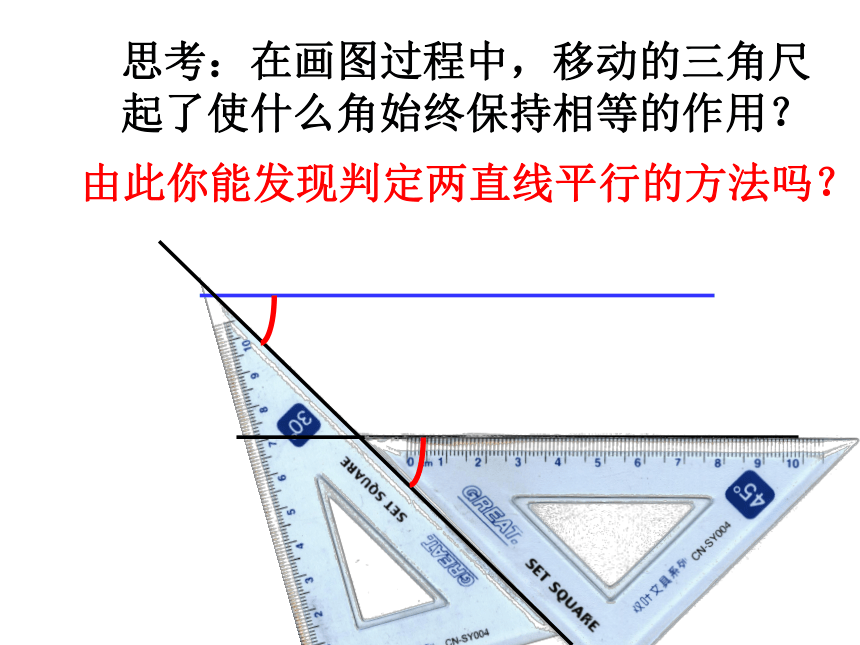
思考:在画图过程中,移动的三角尺起了使什么角始终保持相等的作用?
由此你能发现判定两直线平行的方法吗?
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行
简称
∵∠1=∠2
∴
a
∥
b
(
)
几何叙述:
同位角相等,两直线平行
1
a
b
c
2
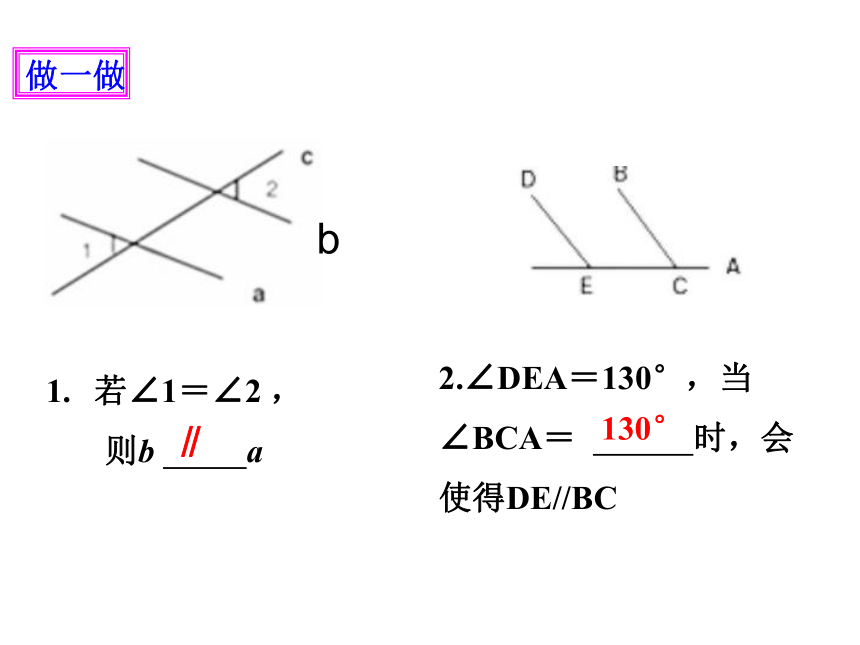
做一做
若∠1=∠2
,
则b
a
∥
2.∠DEA=130°,当
∠BCA=
时,会
使得DE//BC
130°
b
4
1
2
3
A
B
C
E
F
D
5
H
G
3.如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
4.如果
,
能判定哪两条直线平行?
∠1
=∠2
∠2
=∠5
∠3
=∠4
做一做
例
1
如图,直线l1
,l2被直线l3所截,
∠1=45°,∠2=135°,
判断l1与l2是否平行,并说明理由.
已知直线
被
所截(如图)
,
,判断
是否
平行,并说明理由.
变式1
已知直线
被
所截(如图)
,
判断
是否平行,并说明理由.
变式2
垂直于同一条直线的两条直线互相平行
在同一平面内,
变式3
2
1
1.如图,已知直线
,
被直线AB所截,AC
于点C.若
则
与
平行吗?
请说明理由.
A
B
1
2
C
练一练
2、如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,
∠ABG=30°。请判断AE与CD是否平行,并说明理由。
练一练
1、某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图)。这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由。
A
B
C
15°
1
2
D
E
拓展训练
拓展练习
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
A
B
C
D
E
F
G
1
2
试一试
如图,哪些直线平行,哪些直线不平行?请说明理由.
50°
60°
120°
l4
l3
l2
l1
小结
通过本节课的内容,你有哪些收获??
(1)同位角相等,两直线平行.
(2)在同一平面内,垂直于同一条直线的两条直线
互相平行.
2、用“同位角相等,两直线平行”判定两直线平行,能进行简单的推理和表述.
1、判定两直线平行的方法:
1.3平行线的判定(1)
教学目标
从“用三角尺和直尺画平行线”的活动过程中发现基本事实:同位角相等,两直线平行。
掌握基本事实:同位角相等,两直线平行。
会运用基本事实及其推论判断两直线平行,会进行简单的推理和表述。
教学重点
掌握“同位角相等,两直线平行”的判定方法
教学难点
例1中,需先将已知条件作适当的转化,说理过程要求有条理的表述。这方面能力,学生较薄弱。
温故知新
(1)平面内两条直线的位置关系有几种?
(2)过已知直线外一点画已知直线的平行线
完成P11作业题4
一、贴
二、靠
三、推
四、画
平行线的画法:
思考:在画图过程中,移动的三角尺起了使什么角始终保持相等的作用?
由此你能发现判定两直线平行的方法吗?
平行线的判定方法1:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
同位角相等,两直线平行
简称
∵∠1=∠2
∴
a
∥
b
(
)
几何叙述:
同位角相等,两直线平行
1
a
b
c
2
做一做
若∠1=∠2
,
则b
a
∥
2.∠DEA=130°,当
∠BCA=
时,会
使得DE//BC
130°
b
4
1
2
3
A
B
C
E
F
D
5
H
G
3.如图,哪两个角相等能判定直线AB∥CD?
1
4
3
2
A
D
C
B
4.如果
,
能判定哪两条直线平行?
∠1
=∠2
∠2
=∠5
∠3
=∠4
做一做
例
1
如图,直线l1
,l2被直线l3所截,
∠1=45°,∠2=135°,
判断l1与l2是否平行,并说明理由.
已知直线
被
所截(如图)
,
,判断
是否
平行,并说明理由.
变式1
已知直线
被
所截(如图)
,
判断
是否平行,并说明理由.
变式2
垂直于同一条直线的两条直线互相平行
在同一平面内,
变式3
2
1
1.如图,已知直线
,
被直线AB所截,AC
于点C.若
则
与
平行吗?
请说明理由.
A
B
1
2
C
练一练
2、如图,AB⊥CD于点B,AE与BF相交于点G,且∠FGE=60°,
∠ABG=30°。请判断AE与CD是否平行,并说明理由。
练一练
1、某人骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图)。这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由。
A
B
C
15°
1
2
D
E
拓展训练
拓展练习
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
A
B
C
D
E
F
G
1
2
试一试
如图,哪些直线平行,哪些直线不平行?请说明理由.
50°
60°
120°
l4
l3
l2
l1
小结
通过本节课的内容,你有哪些收获??
(1)同位角相等,两直线平行.
(2)在同一平面内,垂直于同一条直线的两条直线
互相平行.
2、用“同位角相等,两直线平行”判定两直线平行,能进行简单的推理和表述.
1、判定两直线平行的方法:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
